A current carrying wire is taken to be a prime magnetic source. A straight infinitely long wire is shown to be equivalent to a single positive charge (the ions) and a single negative charge (the current electrons) positioned at the wire directly opposite a test charge. Relative to a moving test charge the electric fields of these two charges are modified by the Lorentz Transform equations. The additional velocity of the current electrons causes the two fields to differ such that a net non-zero field results. This net field causes an acceleration of the test charge at 90degs to its velocity. This derivative of the electric field we call magnetism.
It is understandable that magnetism and electrostatics were initially considered to be separate forces with totally different origins. After all a magnet has no effect upon a charged body and vice-versa.
But in 1870 James Clerk Maxwell discovered a connection. Depending upon the observer's relative velocity to the source a magnetic effect could appear to be an electric effect--and vice versa. Maxwell developed his famous equations of electromagnetism which inter-relate the two effects, giving each equal relevance. For example, in the electromagnetic wave the magnetic and electric forces, act at 90degs to each other with equal significance. Thus Modern Physics has a schizophrenic view of the electric and magnetic effects. In the electromagnetic wave they are separate but connected effects. Elsewhere one effect may act as the other effect depending on the relative velocity of the test body.

An electric current through a wire creates a force field around the wire called the magnetic field. When the wire is formed into a circle, or indeed into many turns as in a solenoid, it exactly emulates the effect of a permanent magnet.
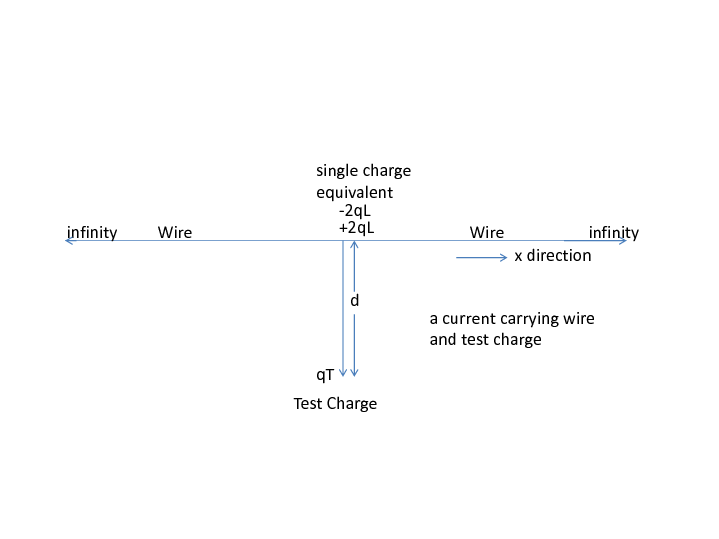
Consider the effect of a straight current carrying wire of infinite length (the x direction) upon a single test charge of unit value positioned at a distance d ( in the y direction) from the wire (shown above).
The wire consists of an equal number of positive ions and current electrons of which the linear density of each is taken to be qL. Each separate charge in the wire creates a force upon the test charge as a function of its distance from the test charge. It can be shown that the net force of all the positive ions in the infinite length wire is the equivalent of the electric potential of a single point charge of value +2qL positioned in the wire directly opposite the test charge (the y direction). In this special situation, force and potential are identical.
Similarly the total force of all the current electrons is a charge of -2qL at the same point.
Thus the picture is simplified to a single positive and single negative charge at the same point on the wire line at distance d from the test charge qT.
For the calculations see the book Aether Theory, the pdf is on my
website.
It might be expected that the electric potential field of the charge +2qL is exactly cancelled at all times by the field of the charge -2qL such that the resultant potential (and hence force) on the test charge is zero.
However the effect of velocity on electric fields (see The Electric Field in Aether Physics) must be taken into account.
When the wire ions, current electrons and the test charge are stationary with respect to each other the Aether velocity effects are identical for all. Relative to their own IRF the three fields are perfectly spherical.
However if a current flows in the wire then the current electrons have an additional velocity Vi along the wire and as a consequence the electric field of charge -2qL is length contracted by a small degree in the direction of the wire to the shape of an ellipsoid. The electric field of charge +2qL no longer exactly cancels that of charge -2qL
However the contraction of the field is mainly in the x direction and not in the direction of the test charge.
But now consider that the test charge is not stationary but is also moving relative to the wire in the y direction.
From the point of view of the test charge the relative velocity Vr of the wire causes the electric fields of charges, +2qL and -2qL, to length contract--but now in the y direction.
Hence the electric field of charge -2qL is contracted in two orthogonal directions simultaneously. This causes the field to rotate by a certain degree.
The rotated ellipsoidal field of charge -2qL creates a field contour at the test charge at a small angle to the x direction.
The net result is a field with a component gradient in the x direction.
Thus the test charge experiences an unexpected force at 90 degs to its velocity. This force is called the magnetic force.
The strength of this force may be calculated from the geometry of the rotated ellipsoid (see the book Aether Theory, the pdf is on my
website) giving:-
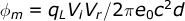
Substituting the current I for qLVi and μ0 for 1/e0c2, and accepting that potential and force are equivalent in this case, we obtain the standard magnetic equation:-
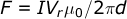
With the test charge moving in the x direction the electric fields of the two charges,+2qL and -2qL will be contracted by the Lorenz function Gr where G is the Lorentz function 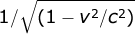 .
.
The current velocity of charge -2qL causes an additional contraction Gi to give a total contraction of GT.
As x = z = 0 the net field at the test charge is therefore:-
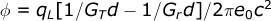
The G factors may be converted by the standard Lorentz Velocity Transform equation:-
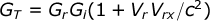
In this case Vrx = Vr as the velocity is entirely in the x direction.
After conversion and taking the relative velocity to be much less than c and the current velocity to be less than the relative velocity we have:-
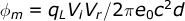
This is exactly the same result for the test charge velocity orthogonal to the wire described above.
Thus the test charge experiences a force at 90degs. to its velocity whatever the direction of that velocity.